This Is Just a Page of Ideas!
Please check any scientific data before use
Folk songs about science are rare, and those found in Minnesota are fewer still. This is not surprising; most people aren’t scientists! We didn’t do much with science in the Minnesota Heritage Songbook; it was designed mostly for use with history or social science classes. But there are a few songs which can be tied in with a science class — notably earth science or chemistry. The following describes several possible labs. Please note: The author has some scientific training (a bachelor’s degree in physics) but no background at all in science education. Nor have I undertaken to try out the labs described here. These are simply suggestions that you will have to flesh out. If you try one, please post a comment on the blog so people can know how it turned out!
Topics
Click on the link to find out about a particular scientific topic and song tie-ins.
A la claire fontaine: Sexual Selection *
The Bayou Sara: Steam Engines and Steam Power *
Charles Guiteau: The Pythagorean Theorem, The Germ Theory of Disease, Air Conditioning *
The Farmer Is the Man: Fertilizer *
It’s A Long Way from Amphiouxus: Evolution *
The Last Fierce Charge: The Minie Ball, Air Pressure, and Spin Stabilization, The Power of Nitrogen *
Lord Franklin: Geography and Navigation, North Magnetic Pole, Global Warming, Lunar Craters, Ice Pressure, Vitamin Deficiency, Solubility of Gases *
The Persian’s Crew: Density of Fresh versus Salt Water *
Pium Paum: Music and Science *
Red Iron Ore and Red River Valley: Glaciation *
Uncle Sam’s Farm: Electromagnetism and the Telegraph *
Young Charlotte: The Square-Cube Law *
A la claire fontaine: Sexual Selection
Why did the nightingale sing his song? To get the lady nightingale.
Of course, lots of birds sing, and it isn’t always for mating purposes. Another common reason is to establish a territory: “This is my tree. Not yours. Mine.” Or to say, “Look out! Enemy!”
But most territorial and warning calls are stereotyped. A chickadee sings “Chick-a-dee-dee-dee-dee-dee” when it sees a human come too close. It doesn’t sing its mating call “whee-hoo.” In chickadee language, specific sounds have specific meanings.
Not to nightingales. They want to sing as many different songs as they can. Because every different song they sing is a signal. They’re saying, “I must be a superior male, I know so many songs!”
This comes about due to a phenomenon known as sexual selection. Charles Darwin first suggested it, but the idea was really popularized by more recent biologists such as R. A. Fisher. The idea is this: One sex (usually but not always the female) prefers some particular trait. Males which have this trait mate with the most females. And suddenly you have what is known as a “runaway process.” In nightingales, you have females who like good singers mating with males who are good singers. The two traits instantly start reinforcing. The next generation has more good singers, and more females who like good singers, so the females can become even more picky about demanding musically gifted mates. And so on, until something starts to slow down the process (usually by placing the displaying male under such a handicap that some sort of balance is reached. In the case of nightingales, for instance, if they spent any more time singing, they probably wouldn’t have any energy left for breeding).

The theory of Sexual Selection argues that peahens mate with the peacock who had the most beautiful plumage in her mind. (Photo credit: Wikipedia)
The nightingale isn’t the only example of runaway sexual selection. Birds seem to be particularly subject to garish examples of this (possibly because a brightly-colored bird can fly away from a predator, which is not an option for, say, a brightly-colored rabbit. Mammals, instead of developing bright colors or elaborate patterns, prefer such things as big heads of antlers or long manes). A notorious example of a sexually-selected creature is the peacock. It has an absolutely absurd tail. Beautiful, yes — but, most of the time, it just gets in the peacock’s way. So why grow such a ridiculous thing? Because peahens like it. Peacocks are raised mostly by their mothers, so a successful male peacock is one who can attract the most mates. Hence the big, goofy tail. Think of it as the peacock equivalent of a shiny red sportscar. (And it doesn’t even contribute to global warming.)
In America, sexual selection is perhaps better illustrated by grouse. Again, it is the females who raise the young. The males do nothing — except that, once a year, they gather at a so-called “lek.” There they display for the females — quite literally, they “strut their stuff,” trying to convince a female to mate with them. In such a short exposure, the female can’t really know much about the male in general — but she knows that he looks good (according to whatever criteria she applies for being good-looking). They mate, and the round of sexual selection continues.

Goldie’s Bird-of-paradise: Ornamented male above; female below. Paradesia decora by John Gerrard Keulemans (d.1912) (Photo credit: Wikipedia)
You can see some of this in bird calls. Although male nightingales do all the singing, it’s not true in other species. Take the Northern Cardinal, a good Minnesota bird. This is a monogamous species: Male and female work together to raise the babies. And — guess what — the females sing as well as the males. The males sing more — but I remember going out one spring morning and hearing a cardinal singing its territorial song “Chew-chew-chip-chip-chip-chip-chip.” Looking, I couldn’t see the bright red bird anywhere. Puzzled, I spent about five minutes searching. Finally, I realized that the female was the one doing the singing. For five or ten minutes. Because they raise the kids together, both male and female cardinals sing the songs.
But it’s always the same song. Unlike the nightingale. Who sings as many songs as he can — because his mother liked other nightingales who sang so beautifully.
You can probably show this on a field trip, if you can pick an area where enough birds are engaged in mating behaviors. Look around for the birds which do the most displaying (by song or feather color) and then check on their mating habits.
It may even be possible to demonstrate this in the lab, although it will take a very in-depth course. In some cases, a species will prefer a particular appearance. Female scarlet tanagers are supposed to strongly prefer the reddest possible mates. Swallows prefer mates with the longest possible tails. And rainbow trout — prefer bright-colored trout. Perhaps a little paint can affect their reproductive success…?
The Bayou Sara: Steam Engines and Steam Power |
 The single most deadly cause of accidents on early steam ships was boiler explosions. The very first steamer to serve on Lake Superior, the Independence, blew up in 1853; it would not be the last boat whose boiler “cooked off.” On the Mississippi, among others, the Frank Steele exploded at La Crosse in 1864. Though none of the Minnesota steamers left a record in song, the Bayou Sara was far from alone in meeting her end due to her own steam engine.
The single most deadly cause of accidents on early steam ships was boiler explosions. The very first steamer to serve on Lake Superior, the Independence, blew up in 1853; it would not be the last boat whose boiler “cooked off.” On the Mississippi, among others, the Frank Steele exploded at La Crosse in 1864. Though none of the Minnesota steamers left a record in song, the Bayou Sara was far from alone in meeting her end due to her own steam engine.
Why the explosions? Because steam is a very powerful thing — that’s why the steam engine revolutionized the world. But steam engines depended on confining gas at high pressure. Too much pressure, or a container not properly vented, could result in an explosions. It’s easy to demonstrate the power of steam; all it takes is a bunsen burner, a flask, water, some tubing, and a balloon. Fill the flask about a quarter full with water (the warmer it is, the faster the experiment will run). Attach the balloon via the tubing — be sure to clamp it tightly, or the steam pressure will blow it off. Light the bunsen burner and boil the water. The balloon will expand, then explode, as the steam pressure builds up.
Note: Do not point the tubing at any of the students; the live steam, once the balloon explodes (which it will do fairly quickly once the water is hot) can easily scald.
Theoretically, you don’t even need the water flask in here; you can demonstrate the power of thermal expansion just by heating air. The expansion follows the famous formula PV=nRT (where P=pressure, V=volume, n=the total gas in the system, R is the gas constant, and T is the temperature on an absolute scale).
You can demonstrate this using the same flask-and-balloon setup as before, though, this time, you’ll want to have a thermometer in there somewhere as well. And you’ll need a flask which can take the heat of the flame. (In the version with the water, the water held the temperature at no warmer than its boiling point. With air in the flask, the whole system will reach a much higher temperature.)
The nice thing about this is that, as long as you have a sealed system, you don’t really need to know n (or R). And even P can almost be ignored, as long as you use a nice floppy balloon (one that doesn’t need much pressure to blow up, such as say a plastic grocery bag). The balloon in that case will end up with a pressure only slightly above room pressure. So the volume of gas in your whole flask-plus-balloon system will vary directly with the temperature. Put a thermometer in the flask (or somewhere), and place a ruler on a clamp behind the balloon. You can measure the increase in the balloon’s volume as the temperature increases.
This experiment requires caution, just like the one with the live steam. Hot air is not as dangerous as steam, because its thermal capacity is smaller, but that also means it heats up faster! Your balloon will probably pop fairly quickly, and that will release some fairly hot air. Also, be sure that you use a plastic that will not melt.
Charles Guiteau: The Pythagorean Theorem
There are lots of presidential trivia books out there. One I’ve seen is called something like “Which President Killed a Man?” Since quite a few Presidents have been generals (Washington, Jackson, Harrison, Taylor, Grant, Hayes, Garfield, Eisenhower) and quite a few others have been soldiers (including Theodore Roosevelt, who in effect charged up San Juan Hill to the White House), the answer is surely “Lots of them.” But if the question is, “Which president invented a new proof of the Pythagorean Theorem,” there is surely only one: James A. Garfield (Crease, p. 30).
The Pythagorean Theorem is, of course, the rule relating the sides of a right triangle. The rule is that, if the legs of the triangle (the sides next to the right angle) have lengths a and b, then the length of the hypoteneuse c can be determined according to the formula a2+b2=c2. This rule, or something like it, seems to have been known to many ancient peoples; Pythagoras’s contribution — if indeed it was his — was to provide a rigorous mathematical proof.
These days, the usual proof is not that of Pythagoras but that of Euclid. Without going into full detail, the diagram below shows the basic sketch of the Euclidean proof. Euclid constructed squares from the three sides of the triangle (in the diagram, the standard 3:4:5 triangle, so the squares have areas 9, 16, 25).
Euclid’s proof started by drawing a line perpendicular to the hypotenuse through the vertex C (shown here as a red line, CX). This divides the square constructed on the hypotenuse (here, the 25 unit square at the bottom of the diagram) into two rectangles. Euclid’s proof showed that the area of the smaller rectangle was equal to the area of the square constructed on the shorter leg, while the area of the larger rectangle was equal to the area of the square constructed on the larger leg. Therefore the area of the larger square, which of course is equal to the sum of the areas of the two rectangles, must also be equal to the areas of the two smaller squares.
This is the most famous proof of the Pythagorean Theorem — a theorem which is famous and important because it was one of the very first mathematical results to be rigorously proved (as opposed to merely observed and treated as true). But most mathematical results are susceptible to proofs in many ways — there are supposedly several hundred different types of proof of the Pythagorean Theorem, although most of them involve mathematics which would be considered more advanced than simple right triangle geometry. People still construct new proofs of the theorem as a mental exercise. And one who did so (in 1876) was future president Garfield, widely regarded as one of the cleverest men ever to become president (he learned to read at the age of three!). Garfield’s working diagram is shown here; can you see how to use it to construct a proof? (Honest admission: I didn’t see it when I saw the diagram. But I’ve never been good at geometry.) It is item #231 in the collection of proofs of the Pythagorean Theorem published by Elisha S. Loomis.
It’s perhaps worth noting that the Pythagorean Theorem is actually a special case of the so-called Law of Cosines, which can be used to determine the lengths of the sides of any triangle: c2=a2+b2-2abcos(θ). A right triangle is one with an angle equal to 90° — that is, an angle of π/2 radians. If we set θ equal to π/2 in the above equation, of course, cos(π/2)=0, so the law of cosines simplifies to the Pythagorean Theorem in the case of a right triangle.
Another interesting property is that there are infinitely many integer solutions to the equation c2=a2+b2, with the most famous being a=2, b=4, c=5 and a=5, b=12, c=13. But Fermat’s Last Theorem (now, finally, proved) says that the equation cn=an+bn has no integer solutions a, b, c if n is larger than 2! The proof of Fermat’s conjecture is of course far beyond what we can address here. But the fact that it is essentially the same sort of equation as the Pythagorean Theorem shows how mathematics can so easily be generalized.
Charles Guiteau II: The Germ Theory of Disease
Charles Guiteau shot James A. Garfield on July 2, 1881. It took Garfield two and a half months to die — he did not expire until September 19. What’s more, Rutkow, pp. 138-139, says that Garfield would surely have lived had the assassination taken place today. Rutkow, a professor of surgery, notes that Garfield would have been quickly taken to a hospital, treated, and sent home in fairly short order to make a full recovery.
So why did Garfield die?
Disease. Doctors were constantly feeling around in his wounds. With dirty hands! This “probing” slowed healing and caused his wounds to become infected. Garfield did not die of his wounds; he died of his doctors.
It didn’t have to be so. Garfield’s doctor had been a successful surgeon during the Civil War — but “successful” was a relative term for surgeons of that period. Roughly half the patients who underwent surgery in 1864 would suffer a septic infection as a result, and many would die of gangrene or other illnesses.
Then, in 1865, Louis Pasteur suggested that living things caused infection. He did not prove the “germ theory” until a few years later, but in that year a surgeon, Joseph Lister, heard Pasteur’s hypothesis and thought it sensible. He also heard that carbolic acid (phenol) seemed to control certain diseases transmitted by cattle droppings. Lister started to use carbolic acid as a disinfectant, and by 1867 was able to show that this almost eliminated sepsis.
A decade later, Robert Koch demonstrated that steam could be used to disinfect surgical instruments. Thus medicine had been completely revolutionized between 1865 and 1880. In England and in Germany, surgery was safe.
But in the United States, the revolution had largely been ignored. Younger doctors kept their hands clean, but their elders insisted on keeping their dirt. And they inflicted it on Garfield, and it killed him.
Charles Guiteau III: Air Conditioning
These days, it is almost impossible to imagine living without air conditioning. But air conditioners are a recent invention. President Garfield was said to be the first American to experience air conditioning — but it came too late to help him.
What Garfield experienced wasn’t really what we would consider air conditioning — it was a fan, a bunch of wet towels, and ice used to cool air and blow it upon him. The machine had no actual cooling component. But the idea used in a modern air conditioner had already been advanced by Nicolas Léonard Sadi Carnot (1796-1832), usually known as Sadi Carnot. This took advantage of the gas law PV=nRT (for more on this, see the entry on The Bayou Sara and steam engines). To vastly oversimplyify, most cooling machines start with a gas or liquid in a sealed container at roughly ambient temperature. This gas is then placed under pressure. Since PV=nRT, and n and R are constant in a closed container, this means that an increase in pressure results in an increase in temperature. So we now have a hot fluid in a cooler environment. This hot fluid is allowed to cool back down to ambient temperature, and the pressure is released. PV=nRT applies again: If the pressure goes down, and V, n, and R remain the same, then the temperature of the fluid has to decrease. So, voila, you now have a cool fluid which can cool off something else.
Unfortunately, cooling engines are not very efficient — for two reasons. First, the ideal Carnot cycle requires an ideal gas with a high heat capacity, and there are no such gases (the gas which comes closest to being ideal, helium, has a low heat capacity; those with high heat capacity generally do not follow the gas law very well). Second is the simple mechanical inefficiency of all these compressions and releases and pumping from place to place: It takes a lot of energy to do all that, and the second law of thermodynamics adds inefficiencies at every stage. This is why air conditioning a house is so much more expensive than heating it, even when heating with electric heaters: The electric heaters just pump out heat, at high efficiences, but air conditioners merely move heat at low efficiency. Try as we might, we can’t overcome the second law….
The Farmer Is the Man: Fertilizer |
Although the Grange is best remembered as a political and social group, that was not Oliver H. Kelley’s original purpose. His most important goal was to teach scientific farming. By which we mean mostly “farming using the right fertilizers.”
The use of fertilizer is not a new idea. The use of manure to improve crop yields goes back to prehistory. But sometimes there isn’t enough manure to go around. This was true in the pre-Civil War Old South, for instance — many of the cotton lands of the far east had been completely worn due to overcultivation. A planter named Edmund Ruffin (later a famous secessionist leader) would show that worn-out soil could be revived by adding marl (a mixture of clay and calcium carbonate, usually from seashells; it probably served as a calcium source).
The scientist Justus von Liebig (1803-1873) was the first to determine what was going on. He showed that plants extracted elements from the soil as they grew. (He also earns credit for being the first to determine the calorie contents of foods.) From there he went on to create the concept of artificial fertilizers — of human-made compounds to supply the plants’ needs. His own custom fertilizers were not very good — he refused to concede that nitrogen was needed — but he at least had the idea.
Modern fertilizers usually contain three or four elements: Nitrogen (often in the form of ammonium nitrate), phosphorus (needed in particular for DNA), and potassium or calcium. Plants of course require more than just these elements, but these are the ones most likely to be in short supply.
Nitrogen is the trickiest; the others are common enough that it’s just a matter of mining it and putting it in the fertilizer. Nitrogen is common too — the air is full of it — but it’s very hard to extract. Gaseous nitrogen, N2, has a triple bond between the two nitrogen atoms, making a very strong link. The two nitrogen atoms are so firmly attached that for many years the gas was thought to be inert; only in 1894 was it realized that nitrogen was not the same as the truly inert gas argon. There are only a few plants (legumes) that can fix nitrogen on their own. Farmers had known for some time that planting beans would replenish the soil, but no one really wanted to lose a season or two while a field grew beans. Hence the quest for nitrate fertilizers (as we would now describe them).
For many years, fertilizers were made from “fossil” nitrates — the guano of Peru and the sodium and potassium nitrate (saltpeter) of Chile. There was actually a war, the War of the Pacific, fought over the nitrate beds in what is now northern Chile. And, for several decades, guano ships carried the refuse of millions of seabirds to farms around the world. Sailors even sang chanties about the ports of Ilo and Valparaiso, the centers of this trade. (Note the mention of Valparaiso in The Flying Cloud, for instance. Even more explicit is the sea shanty Tommy’s Gone to Hilo, which Ivan H. Walton collected among Great Lakes sailors; Hilo is not the town in Hawaii but Ilo, Peru, the leading nitrate port.)
In the early twentieth century, a German named Fritz Haber finally came up with an affordable process for using atmospheric nitrogen to produce ammonia (NH3). At last nitrates were available as needed — and they were soon to be needed in massive amounts, because nitrates, in addition to being used in fertilizers, were used in explosives. Even early gunpowder (black powder) was mostly saltpeter — potassium nitrate, KNO3. TNT stands for trinitrotoluene. The explosive in the Oklahoma City bombing was based on ammonium nitrate. Almost every major explosive compound has nitrogen in it somewhere.
Possibly there are demonstrations to be done of nitrogen fixing, or of the explosive power of nitrates? (For the latter, see also the material under “The Last Fierce Charge.”)
It’s A Long Way from Amphiouxus: Evolution and Evolutionary Biology
To the tune of “It’s A Long Way to Tipperary”
| Common Version It’s a long way from Amphioxus, It’s a long way to us It’s a long way from Amphioxus To the meanest human cuss. Goodbye, fins and gill slits, Hello, skin and hair! It’s a long, long way from Amphioxus But we came from there. |
Minnesota Version It’s a long way from Amphioxus, It’s a long way to us It’s a long way from Amphioxus To the meanest human cuss. Goodbye, fins and gill, Welcome, skin and hair! It’s a long way from Amphioxus But we came from there. |
Original Text of “Tipperary” It’s a long way to Tipperary, It’s a long way to go. It’s a long way to Tipperary, To the sweetest girl I know. Goodbye Picadilly Farewell Leicester Square, It’s a long, long way to Tipperary, But my heart lies there. |
One of the most common sources of folk song is parody — take an old tune, and twist the words to a new use. Sometimes the result can take on a life of its own; these days, “Mine Eyes Have Seen the Glory of the Burning of the School” is better known than “The Battle Hymn of the Republic,” from which it is taken.
This began with a popular song of the World War I era, “It’s a Long Way to Tipperary,” which according to folklore was written on New Year’s 1912 by Jack Judge to win a bet. It is officially credited to Judge and Harry Williams.
The text listed here as the “Minnesota Version” came to me as a bookmark in a book of folk songs. It was typed on a note card, rather yellowed, with a hand notation implying that it was learned in Missouri around 1922. But the card, and presumably the song, managed to make its way back to Minnesota. The original chorus is said to have been found on a college bulletin board in the early Twenties. The original consisted only of the chorus, but verses were added later, again by an anonymous hand. The text in the Digital Tradition is as follows:
 A fishlike thing appeared among the annelids one day
A fishlike thing appeared among the annelids one day
It hadn’t any parapods or setae to display
It hadn’t any eyes or jaws or ventral nervous chord
But it had a lot of gillslits and it had a notochord.
It’s a long way from amphioxus,
It’s a long way to us.
It’s a long way from amphioxus
To the meanest human cuss.
So goodbye to fins and gill slits,
Hello lungs and hair,
It’s a long, long way from amphioxus
But we came from there.
Well, it wasn’t much to look at and it scarce knew how to swim
And Nerius was very sure it hadn’t come from him.
The mollusks wouldn’t own it and the arthropods got sore
So the poor thing had to burrow in the sand along the shore.
It burrowed in the sand before it grabbed in with its tail
And said gillslits and myotomes are all to no avail.
I’ve grown some metapleural folds and sport an oral hood
But all these fine new characters don’t do me any good.
He soaked a while down in the sand without a bit of pep
Then he stiffened up his notochord and said: “I’ll beat ’em yet.”
They laugh and show their ignorance, but I don’t mind their jeers
Just wait until they see me in a hundred million years.
My notochord will stiffen to a chain of vertebrae
As fins, my metapleural folds will agitate the sea
My tiny dorsal nervous chord will be a mighty brain
And vertebrates will dominate the animal domain.
The song has had an enduring life on college campuses; I’ve now corresponded with six or seven people who sang it in school, and Sam Hinton — a famous folk singer who also had a career in marine biology — recorded it.
Amphioxus is a deprecated name, the “proper” scientific name being branchiostoma, or in common usage, the lancelet. If you casually glanced at a lancelet, you might almost think it’s a wet-looking maple squirt. But these creatures in fact are among the simplest of all chordates — making them similar to (though almost certainly not the same as) the creature that is the common ancestor of all mammals, birds, reptiles, amphibians, and fish. Vertebrates have a spinal cord. The lancelet does not — it’s too simple for that. But it does have nerves, and those nerves are organized in a nerve cord, which is sort of a spinal cord without the bones around it. It also has a notochord — a sort of a spine without the bones. It’s a stiff thing like a sack of jelly, according to Shubin, p. 94. As vertebrates evolved, they invented that wonderful stuff, bone, and started using it for structural support. And the notochord broke up into a series of rings between the vertebrae — the disks of the spine. Thus amphioxus, although not a vertebrate, had the essential parts of what would become vertebrates. It lives in water, and it does have gills, and we did “come from there” — not from any living lancelet species, but from something very like them, perhaps half a billion years ago.
The fins and gill slits of the song were important: The fins eventually developed bones, and those bones became our arms and legs. And from the gill slits would come our head. Our spinal nerves are still rather like Amphioxus’s — but many other parts of its early body have gone on to much bigger things.
It’s interesting to note that the evolution of people is much like the evolution of songs: Parts change with each new singer, but some parts also stay the same.
The Last Fierce Charge: The Minie Ball, The Power of Nitrogen
Europe first learned of gunpowder around the twelfth and thirteenth centuries. Cannon were (probably) in use at the Battle of Crécy in 1346. The French had a usable infantry firearm at Castillon in 1453. By around 1700, infantrymen were all armed with muskets; pikes and spears and bow-and-arrow were history. Yet infantry charges in the face of musket fire still succeeded — as Napoleon would demonstrate so brilliantly at Austerlitz.
In the Civil War, though, infantry charges against field fortifications universally failed. In the whole war, there were only two instances of properly manned fortifications being carried by assault, at Chattanooga and in the “Mule Shoe.” And each was in fact a special case — at Chattanooga, the defenders fled, and at the “Mule Shoe,” the defensive artillery had been taken out and Emory Upton’s attacking force was using a forerunner of infiltration tactics.
Why could assaults that had worked in 1361, or even in 1811, fail in 1861? Because defensive weapons were better. Yes, Napoleon’s and Robert E. Lee’s soldiers both used muzzle-loading single-shot black powder muskets, which at first glance looked very much alike — but in fact they were quite different. Lee’s soldiers had a bullet which was known as the Minie Ball; Napoleon didn’t. And even Napoleon had something that (say) Henry V of England hadn’t had: Quality gunpowder.
The Minie Ball, Air Pressure, and Spin Stabilization
What difference does a bullet make? A lot, when it turns a smoothbore musket into a rifle.
A rifled weapon — that is, one which has a helical groove in which the bullet fits, rotating the projective — has two advantages over a smoothbore. It produces a tighter gas seal, and it spins the bullet. A smoothbore weapon just sort of pushes the bullet out the end, like a pea shooter. A rifled weapon causes the bullet to fit in grooves, causing it to seal the barrel. Realize that gunpowder “explodes” by giving off a lot of hot gas. The pressure of this gas is what pushes the bullet outward.
The advantage of a tight seal is that it holds in the gas, causing more of its energy to go into pushing the bullet. This is something that you can easily demonstrate. The only set-up you’ll need is a tube of some kind, two marbles (one of which fits very snugly in the tube, one of which is much smaller than the tube), and something which can deliver precise doses of high-pressure gas. (There are gadgets for this, though you might be able to rig up something yourself.) The experiment is simple:
Just put the large marble in the tube, and fire off a dose of the gas, and see how quickly it comes out. Then repeat the experiment with the small marble.
If you’ve set this up right, so that there are no leaks, the large marble should come out of the tube at a much higher speed than the small, because the entire dose of compressed air will have pushed it. The smaller marble, even though it (presumably) has less mass, will not be pushed so hard, because the air can just go around it.
But all the power in the world won’t do any good if the bullet doesn’t go the right way. That’s where rifling comes in. This is harder to demonstrate for something like a bullet and gun, but consider the frisbee. What happens if you pick one up and throw it entirely flat? Answer it wobbles, falls off course, and goes nowhere in particular.
Now spin the frisbee when you throw it. You still may not have aimed it in the right direction — but it follows a nice smooth curve. No wobbles. No falling off course. It is spin stabilized.
Spin stabilization is the key to getting things to go where you want them to go. The lack of spin means objects in air can fly any old way. That’s why knuckle balls in baseball are so nasty — they should be called “spinless balls.” A fast ball has lots of spin. A knuckle ball is thrown to have as little as possible. It wanders its way to the batter — which is why it can be so hard to hit.
A rifle is a gun designed to spin a bullet, usually by having some sort of flange on the bullet run along a spiral groove inside the gun. So a rifle lets you actually aim the gun at something, in hopes of hitting it. With the old smoothbores, you just sort of pointed in the general direction of the enemy and hoped. Hence the old cliche about “Don’t shoot until you see the whites of your eyes” — that was about the range at which a musketeer could expect to hit.
The Civil War was the first major conflict in which both sides had rifle muskets. (We call then “rifle muskets” because they were still loaded down the muzzle, like the old smoothbore muskets. A few years later, the Prussians would be the first army to fight with all their troops having true breechloading rifles.) Why did it take so long to adopt rifle muskets?
Actually, there were rifles for centuries before the Civil War. The problem is, it took a very long time to load them. About two minutes, compared to about half a minute for a smoothbore musket. The problem was, like the smoothbore muskets, they had to be loaded from the muzzle end. (No one had yet figured out how to make a breech that was tight enough to hold the gas when the gunpowder fired; the first steps toward solving the problem were taken in the years before the Civil War, but it took some time to bring the resulting products to market.) The muzzle-loading nature of these early rifles meant that the bullet, with its rifling flanges, had to be pushed down a barrel that was no wider than the bullet itself. This was a very slow process.
 The Minie bullet solved that. It was a bullet which had an expanding end. That meant that it could be dropped down the barrel of the gun, like a smoothbore ball (you had to put it in there in the right direction, and ram it down, but that was a lot easier than the old rifles). But, once fired, the bottom end of the bullet expanded, fitting into the rifling grooves and sealing in the gas in the firing chamber. It was such a clever little piece of engineering that you really have to regret that its main use, in the couple of dozen years it was in service, was to kill people. But it shows how just a little improvement in something can make a big difference. The minie bullet (plus rifle grooves) turned the old smoothbore muskets, which had an effective range in the dozens of yards, into rifle muskets, which hit harder, had an effective range of 500 yards or so, and which could actually be aimed. And that meant that a defender in a trench could sit there and bring down attacker after attacker before they could reach him. In 1815, at Waterloo, Wellington’s musketeers could perhaps get off two musket shots at an attacking line of Frenchmen before getting bayonetted — and neither of those shots was likely to hit its target. A man with a minie rifle would get off probably three times as many shots, and the last two or three had a pretty good chance of hitting. No wonder no one ever managed a successful assault on a trench! And no wonder so many died at Fredericksburg. And so, no wonder there was this song.
The Minie bullet solved that. It was a bullet which had an expanding end. That meant that it could be dropped down the barrel of the gun, like a smoothbore ball (you had to put it in there in the right direction, and ram it down, but that was a lot easier than the old rifles). But, once fired, the bottom end of the bullet expanded, fitting into the rifling grooves and sealing in the gas in the firing chamber. It was such a clever little piece of engineering that you really have to regret that its main use, in the couple of dozen years it was in service, was to kill people. But it shows how just a little improvement in something can make a big difference. The minie bullet (plus rifle grooves) turned the old smoothbore muskets, which had an effective range in the dozens of yards, into rifle muskets, which hit harder, had an effective range of 500 yards or so, and which could actually be aimed. And that meant that a defender in a trench could sit there and bring down attacker after attacker before they could reach him. In 1815, at Waterloo, Wellington’s musketeers could perhaps get off two musket shots at an attacking line of Frenchmen before getting bayonetted — and neither of those shots was likely to hit its target. A man with a minie rifle would get off probably three times as many shots, and the last two or three had a pretty good chance of hitting. No wonder no one ever managed a successful assault on a trench! And no wonder so many died at Fredericksburg. And so, no wonder there was this song.
It was truly tragic that hundreds of thousands of young men in the Civil War had to be hit by minie bullets, rather than the newer bullets than came along in the next few decades. Because the minie ball was soft and hollow, it was almost like a scythe going through flesh — if it hit bone, the bone was almost certain to shatter completely. There was no reconstructive surgery possible; the only medical treatment available was immediate amputation above the wound.
And this was the period before real anesthetics; a man undergoing an amputation might get nothing more than a shot of whisky, and stood a good chance of dying of shock.
Even if he survived that, this was also the period before doctors understood antisepsis. A man who suffered an amputation was likely to die of an infected wound. The most noteworthy example of that was none other than Stonewall Jackson. And, later, James A. Garfield, as described above.
The Union’s statistical report says that, during the Civil War, 6159 men were discharged from the army due to amputations. Surely at least half as many died due to amputations as survived to be discharged (there are no clear figures on this). And the Confederates also had their losses due to amputation. So probably 15,000 men who might have survived a wound with another sort of bullet died or were crippled because of being hit by a minie ball.
In 1867, two years after the Civil War ended, Joseph Lister started using carbolic acid as a disinfectant. Infected wounds were a thing of the past (at least until the late twentieth century, when drug-resistant bugs started to become common). For tens of thousands of young men, it was too late.
The Power of Nitrogen
As many people know, it was the Chinese who first discovered gunpowder: The mixture of charcoal (carbon), brimstone (sulfur), and saltpetre (potassium nitrate, KNO3, also sometimes known as nitre).
What isn’t very well-known is that Chinese gunpowder was not very good. It exploded, but not particularly vigorously. It made decent rockets. It wasn’t much good in firearms.
Possible experiment (please note that we have not tried this!): Showing how changing the proportions can change the explosivity of gunpowder mixes.
It is EXTREMELY important to note that you are dealing with an explosive here, and to keep the quantities VERY small. The standard charge of a Civil War era Springfield rifle musket was 60 grains of powder, or about 3.9 grams. We’d suggest using no more than .6 grams in your demonstration. If your equipment cannot allow you to measure accurately to within a tenth of a gram, don’t try this.
Start by creating a powder consisting of .2 grams ground sulfur, .2 grams ground charcoal or other finely-ground form of carbon, and .2 grams of potassium nitrate, and toss a match in it. It will burn, but it won’t give you much in the way of fireworks. It’s even weaker than Roger Bacon’s thirteenth century formula (which was five parts sulfur, five charcoal, seven of saltpetre).
Prepare another mix. Like the preceding, the total is .6 grams of material, but the proportions are different: .1 gram of sulfur, .1 gram of carbon, and .4 gram of potassium nitrate. That will explode — this isn’t too far removed from the earliest forms of gunpowder.
If you really want to make it explosive, the ratio of materials in the nineteenth century had even more saltpetre than the 1:1:4 ratio above; the best mix is on the order of 1:1:6.
Oh, and don’t even think about mixing this stuff up in advance. Damp can cause it to stop working — and, even more to the point, gunpowder can explode. And if that doesn’t convince you, the components can separate if allows to stand. Until about 1430, when the powder mill was invented, black powder had to be mixed in the field. If pre-mixed, it came apart. (This was another reason why modern gunpowder was better than the early forms: It was milled.)
Astonishingly, the key ingredient of this, the saltpetre, is freely available at a home improvement store. It’s called “stump remover,” and it’s typically pure potassium nitrate.
So what makes this stuff go boom? It’s the nitrogen.
Nitrogen is an absolutely necessary element for life; it’s found in DNA, it’s found in the amino acids that make up proteins, and it’s found in lots of other chemicals important for survival. But it’s a strange element — one of its most stable forms is just plain old nitrogen gas, N2. This is very stable because it involves a triple bond — a bond so strong that, until the early twentieth century, no one could commercially extract nitrogen from the gas. Scientists had all the nitrogen they could want — but they couldn’t use it for anything. All nitrates were “fossil” nitrates, chemicals found in some sort of deposit somewhere. And it was only nitrates that were useful; pure nitrogen was just a gas that didn’t even have the good grace to burn.
(The things nations went through to meet their need for fossil nitrogen was amazing — the reason being that they needed so much of the stuff. Britain is said to have imported 20,000 tons of saltpetre per year during the Napoleonic Wars. Little wonder, then, that Britain’s King Charles I, early in his reign, put down an order that people collect the contents of their chamber pots — which could be used in the manufacture of saltpetre. He even created a corps of officials, the “petermen,” to collect the waste. Nor was this the last time this was done. During the Civil War, the South was so desperate for nitrates that appeals were made for the people to save the contents of their chamber pots, which could be processed to yield nitrates — there is actually a folk song about this, called “Chamber Lye.” The North had no need for this; it used primarily the nitrates of the deserts of South America. These were so valuable that, in the late nineteenth century, Peru, Bolivia, and Chile fought the “War of the Pacific” to possess them, even though the land was some of the driest on earth and completely without inhabitants, except nitrate miners.)
Almost all modern explosives are nitrates of one sort or another. Gunpowder was the first, but the ammonium nitrate used in the Oklahoma City bombing is another. (But, no, there is no way to stop using nitrate fertilizers; as the section on fertilizer shows, plants need their nitrates!) The next major explosive to be invented was nitroglycerine. Dynamite is nitroglycerine mixed with a special sort of clay. TNT is trinitrotoluene. Mercury fulminate, considered perhaps the touchiest of all “ordinary” chemical compounds, is Hg(CNO)2. If it’s a chemical explosive, odds are that it involves nitrogen somehow — and, if it blows up, it’s because the nitrogen is coming loose to form N2 molecules.
This was not obvious during the Civil War. Although the Law of Definite Proportions had been established, the idea of valency was still in its infancy, and Kekulé von Stradonitz did not start presenting his chemical structure theory until 1858. It is noteworthy that, soon after that happened, more and more people came up with more and more explosives — known by such names as cordite and lyddite, but they all work by the power of nitrogen.
The most famous of these nitrogen compounds is probably cordite, of which there were several formulations. They are collectively known as “smokeless powders.” They had two advantages over black powder. One is that they tended to have more kick. The other is that there was less residue — hence the “smokeless” part. Civil War battles, using black powder, regularly were shrouded by the stinking clouds of powder residue; the men themselves found their faces coated with black grime from the powder (especially the sulfur part). Smokeless powders typically consisted of components such as nitroglycerine (1,2,3-trinitroxypropane, C3H5N3O9), nitrocellulose (guncotton, C6H7(NO2)3O5 and related forms, which produces enough explosive power that it is used for small rockets such as the classic Russian Katyusha), and camphor (C10H16O). It will be noted that these chemicals contain no atoms other than carbon, hydrogen, oxygen, and nitrogen, whereas gunpowder contains both sulfur and potassium. It is this lack of contaminants that allows the smokeless powders to be (relatively) smokeless: The main products of their explosion are carbon dioxide, water, nitrogen, and perhaps some other combinations such as nitrous oxide. Cordite fumes are not safe to breathe, but (unlike gunpowder) they dispersed quickly and did not significantly obscure the battlefield. As a result, smokeless powders were adopted by all major armies almost from the moment their national chemists came up with a workable formula.
Lest we think that nitrogen compounds can only be used for explosives, we should note that they have many, many “civilian” uses. For example, the first commercially useful artificial dyes were the azo dyes, which still dominate many parts of the dye field. The azo dyes are so-called because they have, somewhere near their centers, a nitrogen-nitrogen double bond. Typical of these dyes is Allura Red (FD&C #40), which typically gives orange soda its color. But they form a large class, used in food, clothing, packaging, and much else.
Lord Franklin: Geography, Navigation, Ice Pressure, Vitamin Deficiency |
Of all the songs in the Heritage Songbook, “Lord Franklin” may touch on the highest number of scientific topics. You may pick out the part of greatest interest from what follows.
Geography, Navigation, Latitude and Longitude

A schematic of Mariner 9, the first spacecraft to make a detailed map of Mars (1971), showing the major components and features (Photo credit: Wikipedia)
If you look at Google Maps, or any recent map of earth, you’ll find it fully mapped. Indeed, you can go out and buy detailed maps, or even globes, of the Moon and Mars. It’s easy to forget that, until 1959, no one had seen the far side of the moon, and until 1971, there were no detailed maps of Mars.
It’s even easier to forget that, when Minnesota became a state, no one even knew whether the North and South Poles were on land or water. The edges of Antarctica were only partly explored, and no one had been a significant distance inland. Ships trying to reach the North Pole had been stopped by ice, and no one knew how far north Greenland and the Arctic Archipelago reached. The interior of Africa was unexplored and unmapped by Europeans; large portions of the Pacific had never been visited.
Part of the reason is that these places were hard to get to. The other part of the reason was that, for most of history, it was almost impossible to make a truly accurate map. Why? Because no one had a way to measure longitude. A good surveyor could determine latitude just by measuring the angle of the sun at noon, but longitude literally had to be worked out by guess-and-hope: A mariner would set a course (which could be done with fair accuracy using a compass during the day, and with greater accuracy by looking at the stars on a clear night), and measure the speed of the ship with other equipment, and work out the east-west distance by trigonometry. It was pretty close to hopeless, because the ship’s speed and exact course always varied. The main reason why there was disagreement over whether Christopher Columbus would be able to sail from Europe to Asia is because, in the fifteenth century, there was no possible way to determine longitude, so no one really knew how far he would have to go. And, because science at that time didn’t really exist, no one really went out to verify the matter.
So forget global positioning systems. The greatest aid to navigation ever created was — a pocket watch. Until the chronometer (a truly accurate device to measure time on shipboard) was invented, it was literally impossible for an explorer ever to know where he was.
Latitude is something you can do as a lab exercise, using a sextant and a calculator. It may come as a shock to realize that the poet Chaucer was actually able to do navigation as it was practiced in his time; A Treatise on the Astrolabe is his instruction to his ten-year-old son on how to calculate latitude. (You can find out more about astrolabes at www.astrolabes.org; astrolabes were used for navigation before sextants came along).
 A good natural history museum store will have astrolabes and perhaps even sextants available, though not the most accurate models. They are also available from places such as Edmund Scientific. You might also find other early navigation equipment such as cross-staves, back-staves, and quadrants (typically used by mariners before sextants were developed).
A good natural history museum store will have astrolabes and perhaps even sextants available, though not the most accurate models. They are also available from places such as Edmund Scientific. You might also find other early navigation equipment such as cross-staves, back-staves, and quadrants (typically used by mariners before sextants were developed).
A sextant is a precision instrument, with advanced optics to allow a very careful measurement of the angle between any two objects. But you can make a low-resolution equivalent (or at least something that demonstrates the principle) using a protractor, a small tube (such as a straw), and a mounting pin, plus a sheet of black construction paper or something to shade the straw. A sextant and an artificial horizon let you measure the angle between the sun and the ground. (You should not, of course, look at the sun while doing this!) If you do it at local noon on a particular day (which you can determine by watching when the sun is at its highest), then you need only the angle of the sun to the earth on that day to determine your latitude. To compute your latitude, simply wait for the time the sun is at its peak (it might be helpful to cheat and look up the time of actual noon). Measure the angle between the sun and the actual horizon (again, do not look at the sun while doing this; to align the sextant with the sun, point the straw in the general direction of the sun, and shine its image on a sheet of paper). (Real navigators preferred observing the stars to observing the sun, but that’s trickier, cannot be done on cloudy days, and of course has to be done after dark.)
If you can do the experiment after dark, it’s even easier to perform, and you won’t so much as need a table of the sun’s elevation. Just find Polaris, and measure its angle with the horizon (you will have to find a place where you can reliably determine the horizon, to be sure; this can be harder than you think. Most of the things I’m so glibly describing are, frankly, harder than they sound, and involve some mathematics I’m shortcutting around; if you really want to do this, get a book on celestial navigation). For this, you can actually look through the straw of your surveying device (which can even be a telescope if you can read off its angle to the horizon). You can find your latitude by subtracting the angle you measure from 90°. This won’t quite be accurate, because Polaris isn’t quite at 90° north, but it’s close enough for a science project. For comparison, the northwest corner of Minnesota is at 49°N. Grand Forks is around 48°N, which is also about where the Minnesota/Canada border meets Lake Superior. Duluth and Fargo/Moorhead are a little south of the 47° parallel. Little Falls is around 46°N. The Twin Cities are around 45°N. Mankato, Rochester and Winona are about 44°N. And Minnesota’s southern boundary is well north of the 43°N line.
It will give you some pause to think that Minnesota’s Northwest Angle exists because the American surveyors who mapped the area couldn’t do a calculation that a ten-year-old could do in the fourteenth century.
It will give you further thought to realize that Columbus “discovered” America because he was too dumb to do what Chaucer did. The ancient Greeks had of course known that the Earth was spherical, and Eratosthenes had measured its circumference in around 240 B.C.E. He did this by determining the sun’s angle at two points directly north and south of each other, and measuring the distance between them. Eratosthenes came up with a figure that was about right — roughly 40,000 kilometers. But another astronomer, Poseidonius, calculated a different figure about a century and a half later, using a method was based on measuring the angle of the star Canopus at various points and calculating the distance between those points. He got the angle wrong, the distance between points wrong, and the result wrong. But the ancient geographer Ptolemy accepted Poseidonius’s number — and this was the figure Columbus used in his arguments for sailing west (Williams, pp. 8-9). The absurdity is that Columbus could have tested the figures of Eratosthenes and Poseidonius. He could have used an astrolabe to measure latitude, and then measured distances, and from that determined the circumference of the earth (at least assuming earth was spherical and not elliptical or some other odd shape). Yet it seems to have occurred to no one to undertake this simple experiment — after all, Columbus lived a century before Galileo invented scientific measurement. By rights, Columbus should have sailed into the sunset and never come back.
Unfortunately, longitude is much harder to calculate than latitude. There are several reasons for this, but the biggest single one is the lack of a universal reference. There is a North Pole, so you can easily calculate the angle between you and it. There is no East Pole or West Pole, so there is no way to calculate an angle from that. The 0° longitude line that passes through Greenwich is simply arbitrary. So, to determine your longitude, you need to know both the position of relevant stars and the exact time. And keeping time on shipboard was almost impossible, since pendulum clocks (the first accurate clocks) were upset by the swaying of the ship. It wasn’t until 1764 that the Royal Navy tested and approved John Harrison’s chronometer, and navigation became an exact science. Calculating longitude using a sextant and chronometer and tables is far too complicated to explain here, but it will give you some idea of how hard it was to explore the Great Lakes in the time of de la Salle, or to follow the rivers in the time of the Voyageurs, to realize that they could never accurately locate themselves on a globe!
Incidentally, there is one other navigation “experiment” that you can do with just a wristwatch, assuming the watch is correctly set to local time (you can probably ignore the error caused by the fact that you aren’t at the center of your time zone, since this isn’t a very accurate experiment, but you do need to correct for Daylight Savings Time). You’ll also need an analog watch; a digital watch won’t do for these purposes. Point the hour hand at the sun. Then take the angle between the hour hand and the figure 12, and bisect it (that is, find the half way point between the two). That angle is due south (to the limit of your ability to measure, of course). (Bowen, p. 25)
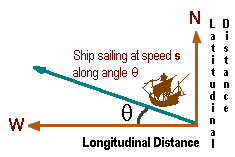 Finally, for those interested in mathematical demonstrations, navigation prior to the invention of the chronometer is an interesting exercise. The method used at the time was “dead reckoning,” which means in essence sailing in a certain direction and figuring out just where you should end up after a certain amount of time. The image at right shows the idea. The angle θ is determined by comparison with the compass or the sun or the North Star; the speed is estimated (or, later, determined by throwing out the log and measuring the speed).
Finally, for those interested in mathematical demonstrations, navigation prior to the invention of the chronometer is an interesting exercise. The method used at the time was “dead reckoning,” which means in essence sailing in a certain direction and figuring out just where you should end up after a certain amount of time. The image at right shows the idea. The angle θ is determined by comparison with the compass or the sun or the North Star; the speed is estimated (or, later, determined by throwing out the log and measuring the speed).
The total distance covered is of course given by the speed s multiplied by the total time t spent following that course. So, if the ship is sailing on a flat surface, the horizontal (longitudinal) distance is given by s·t·cos(θ), and the vertical (latitudinal) distance is calculated by s·t·sin(θ). This can then theoretically be confirmed by using astrolabe or sextant to determine the latitude: If the dead reckoning calculation produces the same latitude that you determine by sextant, then you probably have the longitude correct also.
Of course, a ship will not travel at the same angle and speed for its entire voyage. One simply breaks it down into a series of short legs, and calculates distances for each.
That’s the theory. Have you noticed the practical problem? It’s that the simple calculation involving sines and cosines assumes the voyage takes place on a flat surface. You could probably safely sail a small sea like the Mediterranean that way, but you won’t make it safely across the Atlantic. The answer lies in using spherical trigonometry. Which I don’t intend to try to explain in a music page — but you are free to take it up if you want to.
The problem is easy to demonstrate on a globe. Simply have students start at a given point (say Minneapolis/Saint Paul). On an 18″ globe, I was able to demonstrate this with two legs of 1000 miles; on a 12″ globe, you might need to mark out a journey of 1500 miles on each leg. Have the students mark two routes: One, let us say, 1000 miles south then 1000 miles west. Then mark out another route: On that one, they first travel 1000 miles west, then 1000 miles south. On a planar map, both routes would take you to the same point (one that is about 1400 miles due southwest of the starting point). But try it on a globe: A thousand miles south of the Cities will take you to a point probably a bit north of Baton Rouge, Louisiana (I’m using a piece of string and a globe, just as you probably will, so this is a rather loose approximation). A thousand miles west of Baton Rouge is somewhere around Juarez, Mexico (probably south of it). Now do your thousand miles west from the Twin Cities. That puts you somewhere near the Idaho/Montana border. A thousand miles south of that takes you to somewhere south of Nogales, Mexico (or Tucson, Arizona). The points near Juarez and Nogales have the same north/south latitude, but are separated by hundreds of miles in longitude!
Williams, p. 45, claims that an explorer named John Wood tried to sail the Northeast Passage north of Russia using plane navigation, and ended up losing his ship, though I rather doubt that there is actual cause and effect involved.
North Magnetic Pole
Modern “explorers” tend to make their journeys for reasons solely of fame or self-satisfaction. Think of all the people who climb Mount Everest, or Robert Peary, who headed North Pole expedition after North Pole expedition because, he declared, “I must have fame.”
 It wasn’t always so. The explorers who sought the Northwest Passage were expected to do serious scientific work — Franklin and his second-in-command F.R.M. Crozier were both elected to the Royal Society, and there are lunar craters named Franklin and Crozier. (Of course, Franklin is named for Benjamin Franklin, but they got two for one in that case.) Franklin on his first and second (land) expeditions to the Arctic had been instructed to keep detailed records of meteorological phenomena — and to study magnetism. This was before James Clerk Maxwell, so no one understood what magnetism was. It was known that the magnetic poles did not align with the true north and south poles, but no one knew why, and no one knew exactly where the magnetic poles were located. (It was considered an event when, in 1819, William Edward Parry sailed north of the magnetic north pole; at one time in his voyage, the compass pointed south. Whalers and such had previously found the compass to point mostly west in Baffin Bay, but no one really knew with certainty that this was not some strange effect of being in the north. Parry’s voyage, since it approached the pole from directions not before explored, at last showed that the north magnetic pole was a point, not on the earth’s axis.)
It wasn’t always so. The explorers who sought the Northwest Passage were expected to do serious scientific work — Franklin and his second-in-command F.R.M. Crozier were both elected to the Royal Society, and there are lunar craters named Franklin and Crozier. (Of course, Franklin is named for Benjamin Franklin, but they got two for one in that case.) Franklin on his first and second (land) expeditions to the Arctic had been instructed to keep detailed records of meteorological phenomena — and to study magnetism. This was before James Clerk Maxwell, so no one understood what magnetism was. It was known that the magnetic poles did not align with the true north and south poles, but no one knew why, and no one knew exactly where the magnetic poles were located. (It was considered an event when, in 1819, William Edward Parry sailed north of the magnetic north pole; at one time in his voyage, the compass pointed south. Whalers and such had previously found the compass to point mostly west in Baffin Bay, but no one really knew with certainty that this was not some strange effect of being in the north. Parry’s voyage, since it approached the pole from directions not before explored, at last showed that the north magnetic pole was a point, not on the earth’s axis.)
 So Franklin, on his early expeditions, took not just a compass but an instrument known as a dipping needle. The dipping needle is a three-dimensional compass. There were several models — the simplest was, in effect, nothing more than a magnetized needle hung from a non-magnetic hook. A more precise model consisted of a compass wheel encased in a rotating circle. The inner circle was rotated to point in the direction closest to the pole (i.e. the direction an ordinary compass would point), then the angle of the needle was read. If the dipping needle pointed straight up or down, you were at one of the magnetic poles.
So Franklin, on his early expeditions, took not just a compass but an instrument known as a dipping needle. The dipping needle is a three-dimensional compass. There were several models — the simplest was, in effect, nothing more than a magnetized needle hung from a non-magnetic hook. A more precise model consisted of a compass wheel encased in a rotating circle. The inner circle was rotated to point in the direction closest to the pole (i.e. the direction an ordinary compass would point), then the angle of the needle was read. If the dipping needle pointed straight up or down, you were at one of the magnetic poles.
Franklin did not find the magnetic poles — his early expeditions to Canada kept him too far south. But his friend James Clark Ross reached the north magnetic pole in 1831 — though the expedition almost didn’t get home to report the result.
James Clark Ross, in fact, almost became the first man to reach both the North and South Magnetic Poles. In his 1839-1843 expedition to the Antarctic, Ross tried for to reach the South Magnetic Pole (Michael Smith, p. 100). But the continent of Antarctica blocked him. (In effect, Ross discovered Antarctica. A few points of land were already known, mostly in the Antarctic Peninsula, but Ross was the first systematic explorer of the southern continent)
Interestingly, the location of the magnetic pole has shifted substantially since then. In round numbers, James Clark Ross found the pole at 70°N and 98°38’W. But it was moving! As they stood there, the dipping needle, while pointing almost straight down, was twitching a little. (This is something that is observable only when very, very close to the pole.) At the time, no one knew why — the interior composition of the earth was unknown. (You have to pity James Clark Ross, in a way. He discovered all sorts of things, and gets little recognition for it. The North Magnetic Pole isn’t where he found it, so there is no Ross Museum or the like on the site. The Ross Ice Shelf in Antarctica is named for him — and is vanishing due to climate change. There are many places on the maps which were named by Ross, such as Mount Erebus, the world’s southernmost active volcano, but they aren’t named for him.)
A decade and a half later, Franklin’s men were trapped very close to the north magnetic pole; it was one of the nearest points of land to where their ships were halted. In an odd coincidence, a fellow named W. Parker Snow dreamed of finding Franklin there, and joined a search expedition (though that expedition didn’t go anywhere near the pole). It’s not likely that that inspired this song, but it’s not impossible, either.

Schematic view of the interior of Earth. 1. continental crust – 2. oceanic crust – 3. upper mantle – 4. lower mantle – 5. outer core – 6. inner core – A: Mohorovičić discontinuity – B: Gutenberg Discontinuity – C: Lehmann discontinuity (Photo credit: Wikipedia)
In the years since, the pole has moved dramatically. It is now at about 82°N 118°W.
This suggests several questions a class could examine. For instance, if you stand in your town today and use a compass, how far will its arrow be from true north? And how far off would it have been in 1858 when Minnesota became a state? (You can use the James Clark Ross figure for the pole’s location for this; it’s close enough.)
Also, consider why the pole moves. We now know that the interior of the earth contains a lot of iron. Much of it is semi-molten. This iron is magnetic, but it flows somewhat.
Some of this was known in the time of Franklin and Ross. Henry Cavendish had worked out the mass of the earth half a century before, and this made it clear that the density of the earth as a whole was greater than that of surface rocks. But no one knew what was down there. The motion of the magnetic field is a good reason to study the various layers of the earth — core, mantle, crust. How would you go about measuring the nature of these layers? Why is the iron in the center and the other rocks above it? How does the movement of the magnetic pole teach us about the history of the earth? (Hint: The magnetic poles sometimes reverse themselves — many, many times in the history of the earth, in fact. Using this data can sometimes help us to date rocks and the fossils in them.)
Lunar Craters
Want to get your name on a monument that will not be removed as long as the stars shine and the sun rises? If you’re a famous astronomer or other scientist, it can happen.
Many, many scientists have lunar craters named after them. As mentioned above, there is a crater named Franklin, and another named Crozier. In fact, quite a few craters are named after people involved in the quest for the Northwest Passage. Find a map or photograph of the moon, and see if you can locate these craters.
Amundsen:
Location: 84.5°S 82.8°E
Named for Roald Amundsen (1872-1928), the first man to captain a ship through the Northwest Passage, who was also the first man to reach the South Pole, and the first man who definitely reached the North Pole.
Back:
Location: 1.1°N 80.7°E
Named for George Back (died 1878), a companion of Franklin on his land expeditions, who later conducted a very successful land expedition and a disastrous expedition at sea, which (due to extreme weather) accomplished nothing and barely made it back to the British Isles.
Barrow:
Location: 71.3°N 7.7°E
John Barrow was the second secretary of the Admiralty for most of the first half of the nineteenth century; he organized most of the Northwest Passage expeditions of the period (though he didn’t take part in any of them) as well as other expeditions of exploration. Point Barrow, Alaska is also named for him.
Bellot:
Location: 12.4°S 48.2°E
Joseph-René Bellot was a young French officer who volunteered for the search for Franklin. Liked by almost everyone who met him, he died when ice broke under him and he went into the sea. The Bellot Straight is also named for him.
Crozier:
Location: 13.5°S 50.8°E
Named for the F. R. M. Crozier (1796-1848?), the second-in-command of the Franklin Expedition, who had also been on most of W. E. Parry’s expeditions, and who had been second-in-command of James Clark Ross’s Antarctic expedition. (You can also find various places such as Cape Crozier on earthly maps.)
Franklin:
Location: 38.8°N 47.7°E
Named for Benjamin Franklin, who certainly deserves it more, but let’s pretend it’s for John Franklin as well. (There are quite a few spots on earth named for John Franklin, as well as Lady Franklin Bay on Ellesmere Island. Indeed, part of the Northwest Territories, until they were returned to the Inuit, were named the District of Franklin, after Sir John.)
McClure:
Location: 15.3°S 50.3°E
Robert McClure (died 1873) was the man who eventually was given credit for discovering the Northwest Passage, though he never actually sailed it. He came very close to sharing Franklin’s fate — and deserved it far more. In the early 1850s, several expeditions were sent out to look for Franklin. Two ships, the Enterprise under Richard Collinson and McClure’s Investigator, were supposed to probe from the west. McClure, who had little respect for authority, managed to enter the Arctic first — and, after almost getting stuck in the passage between Banks and Victoria Islands, went north of Banks Island — and got really and truly frozen in. Investigator had to be abandoned, and McClure and such of his men as survived (several had died of scurvy) walked across Viscount Melville Sound to a place where another ship could take them out of the Arctic. He had been very lucky that there were ships in place to rescue him; McClure’s plan (had those ships not shown up) was in effect to abandon his scorbutic men and try to bring the relatively strong sailors out without their comrades.
While McClure was doing this, his superior Collinson had explored the region south of Victoria Island. In doing so, he actually discovered another Northwest Passage, and a usable one (when Amundsen sailed the passage in the early 1900s, he went through the area charted by Collinson, not the area charted by McClure — McClure’s “Northwest Passage” via Melville Sound heads straight into the polar pack and almost never opens up). But Collinson headed back west, and arrived in England after McClure, and so McClure got the credit for the passage. McClure also got a crater, which Collinson did not. Amazingly, there is no crater named for Robert McClintock, either, even though he eventually discovered Franklin’s fate and was in many ways the best English explorer of the nineteenth century. (As in, “Hardly any of his men died.”)
Parry:
Location: 7.9deg;S 15.8deg;W
William Edward Parry (died 1855) was the most successful arctic explorer of the nineteenth century. His first Northwest Passage expedition (1819-1820) made it all the way from Lancaster Sound to Melville Island; no one else would surpass that until Amundsen more than eighty years later. His next two expeditions were less successful (one ended with the loss of a ship), but in 1827 he led a North Pole expedition which made it to 82°45′ north. It would be half a century before another European came that close to the Pole.
Ross:
Location: 11.7°N 21.7°E
This is another “twofer”: John Ross (died 1856) and his nephew James Clark Ross (died 1862). John Ross in 1818 made the first nineteenth century attempt to sail the Northwest Passage by Lancaster Sound — but halted when he saw a mirage that no one else could see. In 1829-1833, he tried again with a semi-private expedition, and managed the amazing feat of keeping his crew alive through four years on the ice. But he himself never discovered anything of note.
James Clark Ross did. As noted in the previous section, he found the North Magnetic Pole. He sailed as a junior officer on most of the other Northwest Passage expeditions as well. And he then led an expedition to Antarctica, exploring large parts of the coast and reaching what was at the time the southernmost point achieved by any human who had ever lived. The Ross Ice Shelf and other Antarctic features are named for him. He could have had command of what would become the Franklin Expedition, but after the Antarctic trip, he decided he had had enough and retired from exploration.
Global Warming
Why was it so hard to find the Northwest Passage in the nineteenth century? Ice.
Almost all the sea water north of Canada froze in the winter (despite being salty!). There was no navigating it then. Only in summer did some of the ice thaw — and even then, it was a matter of finding an open navigable strait. This was so difficult that, though the passage was mapped by the late 1850s, no one managed to actually navigate it until Amundsen in the early twentieth century.
The map below shows most of the various places where nineteenth century explorers were stopped by impassible summer ice.
These days, the Northwest Passage is thawing. The trip that took Amundsen three years, that killed Franklin’s men after four, is now being completed by ordinary hobbyists in three months or less! In 2011, I actually talked to two who made the voyage — Roger Swanson and Gaynelle Templin, who with their crew sailed the Cloud Nine through the passage in 2007. They had a lot of help from global positioning systems and ice reports and such, and of course they had a modern engine and could get fuel along the way (they told me that the passage is still impossible to ships without motors — while they proceeded mostly under sail, they had to use the engine in a few tight spots). But the main reason they got through was not modern technology; it was the clearing of the ice lanes.
Try getting satellite maps of the arctic around July or August, and have your students look for ice-free routes. Then compare these to all the places where nineteenth century explorers were halted by ice.
Ice Pressure
Sailing ships everywhere faced many dangers. Too much wind might sink them; too little would leave them unable to move, at best costing them profits and at worst costing them their lives as their food ran out or they suffered from scurvy (see the next section).
Sailors who went to the arctic faced another danger: Ice. Icebergs were bad enough (just ask the passengers of the Titanic!). But those weren’t the biggest danger of ice in northern climes. It wasn’t even the danger of being trapped. Most years, the ice would thaw eventually, and you could go home.
If you still had a ship. That was the true danger. Ice often tore open ships. Chances are that that is what happened to Franklin’s ships after they were abandoned — and we know that within a generation of the Franklin Expedition, the Jeanette tried to reach the North Pole, and was destroyed by ice, with most of her crew lost or starved as they tried to find their way through Siberia. It’s happened right here in Minnesota, too; the earliest instance in our state seems to have been the Arcola, destroyed by ice at Reed’s Landing in 1857. (In one of those small coincidences that litter history, one of the residents of Reed’s Landing around this time was Charles Nunn, who in 1863 would sell to various members of the Ingalls family the property on which Mary and Laura Ingalls would be born.)
Water is a remarkable compound. Most liquids, when they freeze, get smaller. Water does not; it expands. This is fortunate for things such as lake life, because it means that lakes freeze over rather than freezing through. If we lived on Saturn’s moon Titan, for instance, and our lakes were made of methane, they would always freeze to the bottom. On earth, fish can live under the iced-up surface of the lake — because water expands when it freezes.
(The reason for this is hydrogen bonds — but that’s probably too complicated to be examined in a high school-level chemistry lab. At least, the author knows of no simple experiment to demonstrate hydrogen bonding, even though it’s very important to our lives. Hydrogen bonds also bind DNA together!)
Of course, water’s remarkable traits bring danger with them. The fact that ice is less dense than water means that it floats — and so we have icebergs, and the Titanic disaster. And we also have ships trapped in the ice, and frozen in.
It’s easy to show the destructive power of ice. All you need is a freezer, some sort of a container, such as a metal pan, and something airtight but fairly fragile — a ping-pong ball would work well. Fill the pan almost to the brim with water, drop in the ping-pong ball, and cover the pan with a heavy lid so that the ping-pong ball is forced to be mostly submerged. Then put the whole thing in the freezer, and wait overnight. When you open the freezer the next day, the ping-pong ball will have been crushed.
Ice is amazingly powerful stuff. Just look at all the large boulders and vast amounts of soil that were transported by glaciers.
Vitamin Deficiency
You scurvy rogue!
How many pirate movies have you seen with that line? Have you ever wondered where it came from?
Scurvy is no throwaway line. It was a dreadful disease that killed more sailors than enemy action. A sailor who was away from shore for too long could expect to suffer a condition in which old scars opened and bled, in which the body became weak and the mind confused, in which the gums swelled and the teeth fell out, and which eventually killed. It nearly destroyed Magellan’s voyage around the world. It made sea blockades impossible for many years.
It turns out that the symptoms arose because a man suffering from scurvy could not properly form or maintain collagen. It also resulted in anemia. Depending on a man’s general health and diet, the symptoms usually appeared three to six months after a voyage began. Death followed a few months after.
Pirates often did suffer from scurvy — after all, they were at sea looking for prizes. A scurvy rogue was generally desperate indeed — he was dying!
For many years, no one knew what caused scurvy. Eventually it was realized that fresh food usually cured it. A Scottish physician named James Lind in 1747 conducted an experiment, treating scurvy patients with various substances, and found that citrus juice was effective while most of the other materials were not. It took fifty years or so, but eventually the British Navy as a result began feeding their sailors lemon juice, which proved to be just about the strongest anti-scorbutic available. To make it sound less unpleasant, they took to calling it “lime juice.” Hence British sailors were known as “limeys.” Most of the time, it worked pretty well. Although scurvy had been deadly in the sixteenth through eighteenth centuries, it was very rare in the nineteenth.
 Rare, but not rare enough. The first American settlers sent to Minnesota, the soldiers who would build Fort Snelling, suffered scurvy in the winter of 1819-1820, since they had no fresh food of their own and could not acquire any from the Indians (Ziebarth/Ominsky, p. 7). And although we know almost nothing of what went on during the Franklin Expedition, we do know that, when they abandoned the ships, they still had at least some food. Yet the men died, in droves.
Rare, but not rare enough. The first American settlers sent to Minnesota, the soldiers who would build Fort Snelling, suffered scurvy in the winter of 1819-1820, since they had no fresh food of their own and could not acquire any from the Indians (Ziebarth/Ominsky, p. 7). And although we know almost nothing of what went on during the Franklin Expedition, we do know that, when they abandoned the ships, they still had at least some food. Yet the men died, in droves.
Different scholars have proposed many reasons. Lead poisoning. Botulism in their canned goods. Seasonal affective disorder on a grand scale. Some of these may have applied. But something else certainly applied: Scurvy.
At the time of the Franklin Expedition, the compound in fresh food that cured scurvy had still not been isolated. We now know it as Vitamin C, or ascorbic acid (so-called because it cured scurvy — the name comes from a-scorbic, no-scurvy). It is a simple chemical, C6H8O6. Unfortunately, it is not very chemically stable. It decays over time, especially if exposed to heat or light.
By the time Franklin’s men abandoned their ships, their lemon juice would have been almost useless. Many men seem to have just lain down and died. It is the picture of scurvy.
It wasn’t until the twentieth century that the dietary disease problem was really solved. A Polish-born American biochemist named Casimir Funk (1884-1967) was probably the biggest force in this search. He was the first to isolate niacin, which he called a “vitamine” because it contained an amine group. As it became clear that not all dietary factors contained amines, the name was changed to “vitamin.” Funk would later find the formula for thiamine, and discover a way to synthesize it.
Funk did not isolate the anti-scorbutic vitamin, though. American chemist Charles Glen King was the first to announce it, in 1932. The compound was synthesized by the English chemist Sir Walter Norman Haworth and the Polish-born Tadeusz Reichstein in 1933-1934, making Vitamin C supplements possible. If there were a Franklin Expedition today, it would truly be safe (not that there would ever have been a mystery about its fate, since it would have had radio).
It is interesting to note that, in the process, both white rats and guinea pigs were first used for dietary tests. Guinea pigs were particularly important in the search for Vitamin C; other than primates (monkeys, apes, and humans), they are the only mammals known which cannot synthesize their own vitamin C. So they are the only other mammals subject to scurvy.
The use of letters for the names of vitamins goes back to another American biochemist, Elmer Verner McCollum. He discovered two necessary dietary factors, one fat-soluble and one water-soluble, which he called “A” and “B”. These letters were combined with Funk’s “vitamins” to give us Vitamin A and Vitamin B.
Of course, there were more than just two vitamins — indeed, more than two each of fat- and water-soluble vitamins. Eventually the convention came to be that fat-soluble were given letters (so we have fat-soluble Vitamin A, Vitamin D, and Vitamin E). The water-soluble vitamins were given a number within the B complex. So thiamine became Vitamin B1, while riboflavin is Vitamin B2, and we also need such things as Vitamin B6 and Vitamin B12. (If you’re wondering about missing letters and numbers, such as Vitamin B4 or Vitamin F, chemicals were assigned these symbols but proved either to be identical to previously-discovered vitamins or to not be biologically necessary.)
Solubility of Gases
Here’s a question for you: Why in the world were whales so common in Baffin Bay, which is incredibly cold and dismal; hardly anything lives on land at those latitudes!
The answer: Dissolved oxygen. Cold water holds more gas in solution than hot. The small creatures that feed the whales use the oxygen. Thus, although the waters of Baffin Bay are very cold, they provide much more food than the oxygen-starved warm water farther south. And the cold does not affect whales as much as smaller mammals, because of the square-cube law (saying that the volume of a creature increases as the third power of its length, but its surface area increases only as the square. Thus whales, being big, don’t lose heat as fast as a similarly-shaped small creature. For more on this, see The Square-Cube Law).
There are a number of experiments which can be done to show that the amount of gas dissolved in water decreases as the temperature increases.
The Persian’s Crew: Density of Fresh versus Salt Water
The Great Lakes are famous for shipwrecks. I have four books on the subject: William Ratigan, Great Lakes Shipwrecks & Survivals, revised edition, Eerdmans, 1977, which refers to the wreck of the Persia and implicitly to this song; Mark Bourrie, Many a Midnight Ship, University of Michigan Press, 2005; Michael J. Varhola, Shipwrecks and Lost Treasures: Great Lakes, Globe Pequot Press, 2007 [listed as copyright 2008, but I bought my copy in November 2007]; Mark L. Thompson, Graveyards of the Lakes, Wayne State University Press, 2000. If I wished to add books devoted primarily to the Edmund Fitzgerald, I could easily quadruple the collection.
Why were there so many wrecks? Some of it was the Alberta clippers, and the lack of accurate weather forecasting. Stan Rogers in his song “White Squall” wrote that the waters of Lake Superior could “go from calm to a hundred knots so fast they seem enchanted.”
But another reason is that a ship sailing on the Great Lakes, which are fresh water, will have less reserve buoyancy than a ship sailing salt waters. This hints at several possible experiments to teach good lab technique.
The terms “salt water” and “fresh water” are somewhat vague. Even the freshest water in has some dissolved minerals, and the saltiness of the world’s seas varies. The Black Sea, fed by rivers, is almost fresh; the Red Sea, though relatively close by, evaporates vast amounts of water and is much saltier than the other oceans. But a “typical” sample of ocean water contains 19,000 parts per million of chlorine by weight, and 16,000 ppm of sodium, about 1250 ppm of magnesium, 900 ppm of sulphur, and 400 ppm of calcium and potassium. This means that sea water is roughly 3% more dense than an equivalent volume of fresh water.
To give a practical example: One liter of fresh water at standard temperature and pressure will have a mass of exactly one kilogram. But one liter of sea water will have a mass of between 1.03 and 1.04 kilograms.
There are two ways you can demonstrate the effects of all those dissolved salts. (Well, technically three, since you can also measure electical conductivity — salt water is much more conductive than distilled water. But we’re considering physical properties, not electrical.) One is the direct approach, and may be used to test students’ laboratory skills. Simply give them a given quantity of fresh and salt water, and have them measure the difference in density. (You could even have them determine, by measurement, which is fresh and which is salt, but unless you can seal the containers, this leads to the problem that they can find out by just tasting the water.) You can make this a good test by using different amounts of salt in the “salt water,” so the students can’t just guess at the density.
The other is to actually demonstrate how the difference in densities matters. To do this, you will need a small floating model of a ship or something equivalent; two pans (“oceans”), preferably of glass; salt; water; and some food coloring.
Fill one pan about two-thirds full of fresh water, and add enough food coloring to make it distinctly colored. (The idea is to have enough food coloring in the solution to mark the sides of your toy ship.) Fill the other pan with an equivalent amount of salt water. (For these purposes, you should probably make the water as salty as you possibly can.)
With your students present, gently place the toy ship in the fresh water tank, and allow the water to settle. The food coloring will mark the waterline — that is, it will show how far the ship will settle into the water. (Depending on the type of food coloring, you may want to mark this waterline when you pull the ship from the water.) Then, very gently, place the ship in the salt water pan. The ship will float higher in the salt water (the more salt you put in it, the higher it will float). You will there be able to see that the waterline when the ship is in salt water is lower down her side than in the fresh water.
Note: You should probably make it clear that a boat sailing on fresh water, if it is damaged, will not sink faster or slower than a ship sailing on salt water that is holed at the same point on the side. Yes, a ship on the salt ocean will take on a greater weight of water through the hole, because the salt water is denser. But the ship is floating on salt water, so the buoyant force of the water outside the ship is equal to the downward force of the water inside the ship. It doesn’t matter what fluid is pouring into the ship; the only thing that determines the rate of sinking is how quickly it enters the vessel. The point is not how quickly a ship will sink; it is simply how low it is in the water. When a ship passes from the Great Lakes into the Atlantic Ocean, it will rise higher in the water; when it goes into the Lakes from the ocean, it will ride lower. This means that an equivalent weak spot can potentially let in more water on the lakes.
There is another effect of the water of the sea being salt, and that’s that it freezes at a different temperature. This phenomenon will be very familiar to Minnesotans: It’s why we put salt on the roads in winter. Salt water stays liquid at lower temperatures than fresh, so pouring salt onto ice can cause it to melt and run off the road. Similarly, sea water doesn’t freeze at the same temperature as fresh water (-2°C vs. 0°C). This means that a ship on the Great Lakes also ices up more easily than one at sea.
Pium Paum: Music and Science |
Do you ever wonder why we like music? There is no obvious biological advantage to it — if you wander around singing, you’re that much more likely to be spotted and killed by a lion or hyena (or even a silent human murderer who is out looking for you).
We do not have an answer to this question. There are several hypotheses — one connects music with the sounds we make when addressing children, which are now known to follow distinct melodies. Another thinks music is the framework for dance, and dance is a community-creating activity. Or it might be that music is strongly associated with most religions, and religions help regulate moral behavior and so allow societies to function. Possibly birds pre-defined the tones for us: We like the music of songbirds, which they sing when there is no great danger about; we dislike the croaks and caws of birds like crows, which indicate trouble or dead bodies. Or maybe music, being a strongly mathematically coded activity, was something that simply allowed us to bootstrap higher thinking.
What is clear is that the study of music was one of the earliest scientific activities.
It began with Pythagorus (of Pythagorean Theorem fame) and an instrument we now call, somewhat misleadingly, a “monochord.” (A better name would be a “monotone” — the point being that it produces one tone.) A monochord was simply a single taut string (presumably of gut; these days, we’d normally use metal), ideally placed over a sound box to amplify the sound. (The sound box can be almost anything — a shoebox with a circular hole cut in the top, e.g.)
If by chance you can find a mountain dulcimer around, it makes an ideal “monochord demonstrator,” since the soundbox assures that you can hear the sounds clearly. But if you don’t have a dulcimer around, the principle of a monochord is easy. You just need a string (or metal or gut, not fiber!), something (perhaps weights tied at both ends) to make it taut, two bridges (dowels, say) for it to pass over, and a meter stick or something equivalent to let you measure intervals:
 The principle of Pythagoras is that a vibrating string makes sounds, and that shortening the string by regular whole number intervals makes pleasant sounds.
The principle of Pythagoras is that a vibrating string makes sounds, and that shortening the string by regular whole number intervals makes pleasant sounds.
This was one of the first indications that the universe was regular — that it followed fixed rules. Because it didn’t matter how long the string was, or how high its tension: If you shortened two strings by the same fraction, the two strings saw their tones adjust by the same amount.
This is really easy to demonstrate if you have a mountain dulcimer. You don’t have to be a musician to make this work. Pluck any one of the strings; it will make a tone. Then count up the to the seventh fret (starting from the end with the tuners), and fret the string (that is, push the string down next to the fret. The result is the pleasantly harmonic tone we know as an octave.
If you don’t have a dulcimer, you can achieve the same effect with your monochord by sticking a wedge under the string at just the halfway point. (This is why we constructed it with the ruler under it: So you can easily find the halfway point.) The wedge should be of a size that it firmly stops the string, but does not distort its shape too much.
You can also do this with a guitar, or any other fretted instrument; fret the instrument at the twelfth fret, and pluck it, and you will get a tone an octave above the open string. The difficulty is that, first, it’s hard to play the guitar while it’s flat on its back (which is how you play the dulcimer and monochord), and second, since you have to count up twelve frets, it’s hard to see that that’s halfway up the neck.
It is interesting to note that the typical female voice range is just about an octave above the typical male voice. This means that a man and a woman can comfortably sing an octave apart. This doubtless has significance. But we don’t know what the significance is.
In any case, the octave isn’t the only case where a round number produces a pleasant tone. Suppose we divide our monochord into thirds — equivalent to fretting the dulcimer at the fourth fret, or a guitar at the seventh fret:
This will produce the note musicians call a fifth, or “sol” on the do-re-mi-fa-sol-la-ti-do scale. If we pluck the other side of the bridge, which is one-third the length of the string (eleventh fret on a dulcimer; nineteenth on a guitar) we get the fifth of the octave above the sound of the open string.
Other numbers also produce pleasant tones as well; you can look these up on a music theory web site or in a music theory or physics text — or you can simply play the frets on the dulcimer.
The crucial point here is that all vibrating strings follow these rules. Monochord, guitar, dulcimer, fiddle — it works on all of them. It is this feature — one of the first, if not the first, rule of science to be discovered — which makes stringed instruments possible. And so enables most modern music and dance.
Another branch of science, or at least of engineering, also arose out of the study of musical instruments. An Alexandrian named Ctesibius or Ktesibios (κτησιβιος), who lived probably around 250 B.C.E., invented an early form of organ, which used water pressure to cause air flow through pipes. In working on these organs (hydraulis), he did much experimentation with air and water pressure, and thus can be considered the inventer of hydraulics and pneumatics. He also invented the water clock, the most accurate timepiece available until the invention of the pendulum clock. Unfortunately, his writings are entirely lost; we know of them only at second-hand. So very little that is useful has survived. (It was a genuine tragedy for science that the vast majority of the real science of the Greeks — the works of Archimedes and Ktesibios and Hero, for instance — was lost, while pure speculation such as Plato was preserved in far more manuscripts than was useful. Much of what we know of Greek science is derived from works translated into Arabic and preserved by Islamic civilizations such as the Baghdad Caliphate. But even the Islamic cultures tended to prefer the purely mathematical to the scientific, and it is likely that much that was translated was lost when Islam joined the west in turning away from learning. And even more was surely lost when Constantinople was sacked, first by the Crusaders — who had no respect for learning at all and did most of the damage to the Byzantine libraries — and then by the Ottomans.)
Red Iron Ore and Red River Valley: Glaciation |
Red River Valley | Red Iron Ore |
In the song “Red Iron Ore,” the E. C. Roberts sailed from Escanaba, Michigan to Cleveland, Ohio.
It’s a good thing it didn’t try that trip, say, ten thousand years ago. It wouldn’t have made it.
Why not? Because the Great Lakes have changed very greatly in that time, mostly because of the glaciers.
 At the height of the last ice age, the Great Lakes were entirely covered with ice. Each glacier covered a slightly different area, but most of them extended over all or almost all of Minnesota and surrounding regions.
At the height of the last ice age, the Great Lakes were entirely covered with ice. Each glacier covered a slightly different area, but most of them extended over all or almost all of Minnesota and surrounding regions.
As the glaciers retreated, valleys started to fill with water and the land, which had been pressed down by the ice, started to decompress and rise. The current Great Lakes slowly formed as the ice retreated and rivers started carrying waters into new spots.
The glaciers had reshaped the land. Minnesota’s arrowhead region consists mostly of igneous (volcanic) and metamorphic rocks, which are hard and do not erode easily. (This is the famous Canadian Shield, properly the Laurentian Shield, where the surface is very old because the surface is so hard.) But the rocks of what is now Lake Superior were softer; the glaciers ground much of this material up and carried it south, where it formed moraines in southern Minnesota. The Lake Superior region itself became a hollow cavity which could hold water once the glaciers retreated.
About 11,000 or 12,000 years ago, according to John C. Green’s Minnesota Department of Natural Resources publication Geology on Display: Geology and Scenery of Minnesota’s North Shore State Parks, the ice still covered eastern Lake Superior, the Sault Ste. Marie area, and portions of northern Lake Huron. The western part of what is now Lake Superior was starting to emerge; geologists call it Lake Duluth. Lakes Huron and Michigan covered a much larger area, known as Lake Algonquin. Lake Ontario was much smaller. Only Lake Erie looked roughly as it does now.
Over the next several thousand years, the glaciers retreated dramatically. Lake Erie still looked much as it does today, and Lake Ontario had filled up to roughly its current dimensions. But the upper lakes were much different. Lake Superior had been uncovered, and enlarged toward roughly its modern boundaries, but with a great extension to the north, where waters that would today flow into Hudson’s Bay were trapped. This body of water was known as Lake Minong-Houghton. But the old Lake Algonquin, now far from the retreating glaciers and not filled with the waters of Minong-Houghton, had broken up into three much smaller bodies of water. Lake Chippewa occupied the bottom of what is now the Lake Michigan basin, but it was only about half the size of the modern lake; Green Bay was dry, and Chicago and Milwaukee were far from the ancient shoreline. The central part of Lake Huron was occupied by a body of water called Lake Stanley, but it was much smaller than the current lake, and did not reach anywhere near Detroit. Most of Georgian Bay was a separate lake known as Lake Hough. There was no way to get from Lake Stanley to Lake Erie; instead, Lake Hough and Lake Ontario seem to have had separate outlets to the Champlain Sea, which was a very long, narrow bay reaching up the channel of what is now the Saint Lawrence.
By about six thousand years ago, the northern outlet of Lake Minong-Houghton had closed up, and the water was flowing instead toward Lakes Huron and Michigan. Lakes Superior, Huron, and Michigan were all a large, strangely shaped body of water, covering slightly more area than they do now; Lake Huron had a sort of pod coming off Georgian Bay leading to the Saint Lawrence, as well as a connection to Lake Erie.
After that, the water level gradually lowered to form our current geography.
There are two possible demonstrations you might associate with this. One is to show the effects of differential erosion. You can do this by placing a hard surface next to a softer one (say, baked ceramic tile next to hardened but unbaked clay) and use a surface to abrade it. A brick might work. This would show how the glaciers would wear away soft rock more easily than hard.
The other demonstration is based on the fact that many of the changes to lake geography and level were due to the wearing out of natural plugs. Sault Ste. Marie, for instance, was a blockage point between Lake Superior and Lake Huron. In effect, there was a natural dam there. But eventually the water pressure would blow out the plug, causing water to flow from the upper to the lower body.
To demonstrate this, you would need a sculpted relief map of the lakes area. You could build bottlenecks of, say, sugar or salt. Fill the basins with water, and let the water dissolve the plugs and watch things slosh around. If done right, this can be quite effective. It can also be quite tricky….
We should add that the Great Lakes were not the only bodies of water in Minnesota to be shaped by glaciers. Many of the smaller lakes were also glacier-formed.
And then there was Minnesota’s other Great Lake, Lake Agassiz, which covered a large part of the state in an earlier interglacial period. It was named for Jean Louis Rodolphe Agassiz (1807-1873). Agassiz never visited Minnesota, but it was he who realized that glaciers, instead of being just lumps of ice that sat still at the tops of mountains, could move. His 1840 book Studies on Glaciers introduced the idea of ice ages to the world. Lake Agassiz drained roughly north through the Red River valley, which is one reason why it lasted a long time: A north-flowing river tends to stay in flood in spring because the ice at the northern end of the valley does not melt until late in the year, damming the water as it flows north. But if the Red River had not flowed north, there would likely have been no song about the Red River Valley, because the Hudson’s Bay Company would never have been able to travel up the Red River from Winnipeg.
This is another thing you could do with a model of the landscape. Using clay or some other material, construct two models of a river valley with a large water source at the upstream (higher) end, fill them with water, and freeze the water. Then use a head source, such as a hair dryer or an incandescent light bulb, to melt the water. In one valley, heat the lower part of the river. The water will melt away quite neatly, with little flooding. In the other, heat the upper reservoir and river and watch the flood….
Uncle Sam’s Farm: Electromagnetism and the Telegraph |
The third verse of this song, as found in the Heritage Songbook, runs
Our fathers gave us liberty, but little did they dream
The grand results to follow in the mighty age of steam;
Our mountains, lakes, and rivers are now in a blaze of fire,
While we send the news by lightning on the telegraphic wire.
We tend to think of the telegraph as the work of Samuel Finlay Breese Morse (1791-1872), though most of the basic science derived from the work of Hans Christian Ørsted, and William Cooke and Charles Wheatstone developed a multiple-circuit needle telegraph in 1837. Even Morse’s design owes much to Joseph Henry (1797-1878), who taught Morse the theory he needed (and got no acknowledgement in return).
Still, Morse deserves credit of developing the single-circuit electric telegraph, which he patented in 1840. Within three years he was sending messages from Baltimore to Washington, and by the time of the Civil War, nearly the entire country was “wired.” The telegraph became particularly popular after 1844, when Morse’s associate Alfred Lewis Vaeil introduced the telegraph key.
It is perfectly possibly to build a short-range telegraph in the lab; mostly it requires a power source, a switch or tappable key, and an electromagnet.
Young Charlotte: The Square-Cube Law |
In “Young Charlotte,” the girl freezes and the boy lives. At least at first. The song blames it on the girl’s inadequate clothes, and that probably contributed. But there probably was more to the story. Charlotte, being a girl, was probably shorter than the boy Charlie. And that made all the difference.
Typically, human females are about 10% shorter than males. (There are sound reasons to think this tells us something about our sexual biology, but let’s not get into that yet. Just accept the fact for now.) But the fact that women are 10% shorter does not mean that they are 10% lighter. In fact, a woman of normal height is 30-40% lighter than a man of normal height. Why, if she is only 10% shorter, is she so much lighter?
The difference in bone structure explains part of it, as well as the fact that women tend not to have such bulky muscles (muscles are heavy!), but the primary answer is the Law of Squares and Cubes, or the square-cube law. This says that the surface area of a shape (any shape!) increases as the square of the increase in its linear dimension, and the volume increases as the cube (third power) of the increase in its linear dimension.
So, for example, if you take a cube one centimeter on a side, its surface area is six square centimeters, and its volume is one cubic centimeter.
Now take a cube two centimeters on a side. It’s twice as long (wide, tall). But the surface area is 24 square centimeters. And the volume is 8 cubic centimeters. Thus the surface area has increased by a factor of four, or two squared; the volume has increased by a factor of eight, or two cubed.
Try other multiples, you’ll get the same result. Richard Dawkins suggested that you can actually demonstrate this with sugar cubes: Start with one sugar cube. Now use more cubes to construct a sugar sculpture twice as long, wide, and tall. You’ll need eight cubes. To construct a sculpture three times as long/wide/tall, you’ll need 27. And so forth.
Now think about how the body loses heat when the weather is cold. It’s lost out the surface. The greater the surface area relative to the volume, the faster the body loses heat. Small people lose heat faster than big ones. (This isn’t pure disadvantage, to be sure. In hot weather, they still lose heat faster, so they don’t overheat as easily.)
So here we have big Charlie and little Charlotte, out on a very cold night. Which one is going to freeze first? Charlotte, without a doubt. She might have lasted longer had she dressed better, but she could have worn enough furs to make an Abominable Snowman costume and still been in a lot of trouble.
This, incidentally, is also why whales, which are warm-blooded, can live in some place as cold as Baffin Bay: Being big, they don’t lose heat very fast. Polar bears also benefit from their size. Even though they live an arctic habitat, they actually find themselves getting overheated a lot and have to snuggle up with some nice ice to cool off! (Holmes, p. 93).
This does raise the question of why males are big and females are smaller. The answer is, “We don’t know.” But there are interesting hints (though these are probably things that should probably be saved for an advanced biology class — the kind where you can say the word “evolution” without looking over your shoulder).
It is an interesting fact that primates have extremely diverse mating and cultural patterns. Indeed, just the five primary types of apes (gibbons and siamangs, chimpanzees, bonobos, gorillas, orangutans) all have different behaviors. Gorilla males form harems of up to six females. Orangutans are extremely solitary; males and females come together only to breed. Gibbons and siamangs establish territories and pair bonds, with one permanent pair in each territory — almost like monogamous marriage. Chimpanzees and bonobos form communities, both promiscuous — but of different types. In chimpanzee communities, males are dominant, with strong hierarchies, and females leave their family groups when they mature; the females go into heat; conflict is constant. Bonobo communities are female-dominated; the communities are bonded by sexual favors, and violence is rare.
Humans are, of course, descended from apes — the best guess is that we split off from chimpanzees and bonobos six million years ago (and chimps and bonobos split two million years after that). Gorillas split off perhaps two million years before that, orangutans a few million years before that, and gibbons still earlier.
What is interesting is that, in mammals, and in primates in particular, sexual dimorphism (that is, the ratio between the size of the average male and the average female) seems to correlate with sexual behavior. The larger the dimorphism, the greater the tendency for the male to keep a harem (Dawkins, pp. 205-209). The extreme example of this is not a primate but the elephant seal, where the male has six times the mass of the female and a dominant male may have a harem of as many as forty or fifty females.
No primate has that sort of harem. But gorillas, the only species to keep harems, have a ratio of 2:1 in male size to female size. Chimps and bonobos, which do not keep harems but are promiscuous, have a ratio of 1.3:1. Gibbons, which are (almost) monogamous, have a ratio not much larger than 1:1.
And humans? Humans are 1.2:1 (Johanson and Wong, p. 121). But there are two interesting points here. First, although human males and females are different sizes, their legs are the same length! That is, an average human male is about 10 cm./4 inches taller than a female, but the difference is all in the upper body. This is significant, because it means that males and females have the same natural walking pace (this is determined by the pendulum motion of the leg). Few species with a large sexual dimorphism show this elegant sort of body coordination.
And — even more interesting — the earliest well-documented ancestor of humans after the split from chimpanzees, Australopithecus afarensis (the species which contained the famous Lucy), had a ratio of 1.5:1.
Thus it would appear that human beings have spent the last three million years evolving toward monogamy. We aren’t there yet. But we’re getting closer.
Which, presumably, helps explain why Charlie was so broken up when Charlotte died.
 At Right: A very rough sketch of the relationships between apes and humans, as it was thought to be in 2009.
At Right: A very rough sketch of the relationships between apes and humans, as it was thought to be in 2009.
In the chart, contemporary apes are shown in brown. Members of the genus homo, which would generally be called “human,” are shown in black or grey. Members of the genus Australopithecus are shown in blue-green. Well-established species are shown in dark hues, less-established species in light hues. The red dots represent nodes — that is, places where the lineage split into two or more species. The notation “mya” means “million years ago.” The nodes which separate ape species are based on protein comparisons and may be considered fairly firm; the nodes separating humans and australopithecines are based on fossils and subject to revision as more fossils are found.
The chart shows the creatures in loosely chronological order based on time of existence and extinction. Humans, bonobos, chimps, gorillas, orangutans, and gibbons survive today (although all but humans are in danger of extinction due to loss of habitat). Homo floresiensis probably went extinct between 10,000 and 20,000 years ago. Homo neanderthalensis died off between 25,000 and 30,000 years ago. The others died out before that.
There is no clear distinction between apes, australopithecines, and humans — indeed, some have argued that humans should be classed in the same genus as chimpanzees and bonobos. (There is a genuine problem with this argument, in that humans have only 46 chromosomes and apes have 48; interbreeding is probably impossible — but we don’t know at what stage in the evolutionary process our chromosome 2 formed out of two ape chromosomes, so we can’t really use chromosome count as a way to distinguish). It has been strongly argued that at the very least autralopithecines should be dissolved — either classed with apes or merged with humans. There are however, characteristics which define each genus, if rather loosely. As a rule of thumb australopithecines are bipedal (apes walk or climb with all four limbs) but have ape-sized brains. Humans (genus homo) are australopithecines which have started to develop enlarged brains.
Some species here are much more established than others. Of the existence of Neandertals, Australopithecus afarensis, Homo erectus, and the class of robust Australopithecines there can be no doubt (although many would now split Homo erectus into two species: Homo ergaster, the earlier, which originated in Africa and migrated out, and Homo erectus, an Asian descendent of ergaster. Homo sapiens is considered to be a descendent of ergaster.) Homo habilis, the earliest known member of our genus, is less certain (the fossils of this type are few and very incomplete), and Homo heidelbergensis even less so. Habilis is sometimes treated as a late australopithecine, or an early form of Homo erectus, and heidelbergensis as an early form of modern human. Homo floresiensis, the “hobbit” species only recently discovered, is still hotly contested but the consensus seems to be arising that it is a genuine species, although there is now much discussion about whether it descends from habilis or erectus or something else. The initial opinion was that it must have been descended from Homo erectus, because only erectus made it so far into Asia. But floresiensis has two peculiar traits, an ape-like wrist and a flat foot, which are not found in erectus (or in Homo sapiens). It is these characteristics which are bringing more people around to the view that floresiensis must be a separate species — but they also argue that it must be descended from something earlier in the evolutionary tree than Homo erectus.
Others would add still other species to the tree shown here, such as Homo antecessor between ergaster and heidelbergensis, and Homo rudolfensis, of somewhat uncertain place.
The two most famous early “ape-men,” Java Man and Peking Man, are now classified as Homo erectus.
The Australopithecine genus also include many species, not all of which are shown here. The “robust Australopithecies” are now considered to contain perhaps four species: Australopithecus aethiopicus, Australopithecus africanus (the first known Australopithecine), Australopithecus boisei, and Australopithecus robustus. A species Australopithecus anamensis has been proposed as an ancestor of Australopithecus afarensis, and Australopithecus garhi is suggested as a descendant of afarensis. This will probably be revised as more fossils are found.









